1.
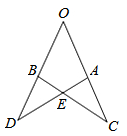
如图,已知OT是Rt△ABO斜边AB上的高线,AO=BO,以O为圆心,OT为半径的圆交OA于点C,过点C作⊙O的切线CD,交AB于点D,则下列结论中错误的是( )

A.
DC=DT
B.
AD=  DT
C.
BD=BO
D.
2OC=5AC
DT
C.
BD=BO
D.
2OC=5AC
【考点】
全等三角形的判定与性质;
切线的判定与性质;
等腰直角三角形;