0 返回出卷网首页
1. 【性质探究】

如图，在矩形ABCD中，对角线AC，BD相交于点O，AE平分∠BAC，交BC于点E。作DF⊥AE于点H，分别交AB，AC于点F，G。

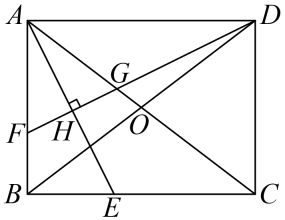
(1) 判断△AFG的形状并说明理由。
(2) 求证：BF=2OG。
(3) 【迁移应用】

记△DGO的面积为S1 ， △DBF的面积为S2 ， 当 时，求 的值。
(4) 【拓展延伸】

若DF交射线AB于点F，【性质探究】中的其余条件不变，连结EF。当△BEF的面积为矩形ABCD面积的 时，请直接写出tan∠BAE的值。
【考点】
全等三角形的判定与性质; 矩形的性质; 相似三角形的判定与性质; 解直角三角形的其他实际应用;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
实践探究题 困难
能力提升
换一批
1. 已知：△ABC与△ABD中，∠CAB＝∠DBA＝β，且∠ADB+∠ACB＝180°.

提出问题：如图1，当∠ADB＝∠ACB＝90°时，求证：AD＝BC；

类比探究：如图2，当∠ADB≠∠ACB时，AD＝BC是否还成立？并说明理由.

综合运用：如图3，当β＝18°，BC＝1，且AB⊥BC时，求AC的长.
实践探究题 困难
2. 如图

(1) [感知]如图①，在Rt△ABC中，∠ACB=90°，点O是AB中点，易知OA=OB=OC，则点A、B、C在以AB为直径的⊙O上．

[应用]如图②，在四边形ABCD中，∠ABC=∠ADC=90°，求证：四边形ABCD有外接圆．
(2)  [拓展]如图③，在四边形ABCD中，∠ABC=∠ADC=90°，AD=CD=4，∠BCD=75°，

连结BD，则∠ABD的度数为，BD的长度为
(3) 如图④，连结AC，将△ABC沿AC翻折得△AEC，连结DE，则∠AED的度数为．DE的长度为
实践探究题 普通
3. 定义：如果四边形的一条对角线把该四边形分割成两个等腰三角形，且这条对角线是这两个等腰三角形的腰，那么我们称这个四边形为“双等腰四边形”。

(1) 如图①，在四边形ABCD中，∠BAD=∠BCD=90°，连结BD，E是BD的中点，连结AE，CE.

①试判断四边形ABCE是否为“双等腰四边形”，并说明理由.

②若∠AEC=90°，求∠ABC的度数.
(2) 如图②，E是矩形ABCD内一点，F是边CD上一点，四边形AEFD是“双等腰四边形”，且AD=DE.延长AE交BC于点G，连结FG.若AD=5，求AB的长。
实践探究题 困难