1.
如图,A、B是⊙O上的两个定点,P是⊙O上的动点(P不与A、B重合)、我们称∠APB是⊙O上关于点A、B的滑动角.
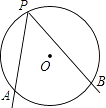
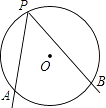
(1)
已知∠APB是⊙O上关于点A、B的滑动角,
(2)
已知O2是⊙O1外一点,以O2为圆心作一个圆与⊙O1相交于A、B两点,∠APB是⊙O1上关于点A、B的滑动角,直线PA、PB分别交⊙O2于M、N(点M与点A、点N与点B均不重合),连接AN,试探索∠APB与∠MAN、∠ANB之间的数量关系.
①若AB是⊙O的直径,则∠APB=°;②若⊙O的半径是1,AB= ,求∠APB的度数;
【考点】
勾股定理;
垂径定理;
圆周角定理;
点与圆的位置关系;
圆与圆的位置关系;


