如图，矩形ABCD（AB＞AD）中，点M是边DC上的一点，点P是射线CB上的动点，连接AM ， AP ，且∠DAP＝2∠AMD ．

0 返回出卷网首页

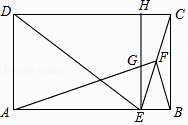
1. 如图，矩形ABCD（AB＞AD）中，点M是边DC上的一点，点P是射线CB上的动点，连接AM ， AP ，且∠DAP＝2∠AMD ．

(1) 若∠APC＝76°，则∠DAM＝；

(2) 猜想∠APC与∠DAM的数量关系为，并进行证明；

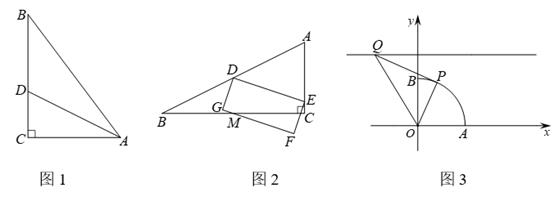
(3) 如图1，若点M为DC的中点，求证：2AD＝BP+AP；

(4) 如图2，当∠AMP＝∠APM时，若CP＝15， $\text{[math]}$ ＝ $\text{[math]}$ 时，则线段MC的长为．

【考点】

全等三角形的判定与性质; 等腰三角形的判定与性质; 勾股定理; 矩形的性质; 相似三角形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 定义：在三角形中，把一边的中点到这条边的高线的距离叫做这条边的中垂距．

例：如图①，在△ABC中，D为边BC的中点，AE⊥BC于E，则线段DE的长叫做边BC的中垂距．

(1) 设三角形一边的中垂距为d（d≥0）．若d=0，则这样的三角形一定是，推断的数学依据是．

(2) 如图②，在△ABC中，∠B=45°，AB= $\text{[math]}$ ，BC=8，AD为边BC的中线，求边BC的中垂距．

(3) 如图③，在矩形ABCD中，AB=6，AD=4．点E为边CD的中点，连结AE并延长交BC的延长线于点F，连结AC．求△ACF中边AF的中垂距．

综合题普通

2. 定义：两直角边比为1：2的直角三角形叫做和合三角形.

(1) 如图1，△ABC中，∠C= $\text{[math]}$ ，AC=3，BC=4，AD平分∠CAB交BC于点D，说明△ACD是和合三角形；

(2) 如图2，和合△ABC中，∠C= $\text{[math]}$ ，AC= $\text{[math]}$ ，点D是边AB中点，点E是边AC上一动点，在直线DE下方构造矩形DEFG，使直线FG始终经过BC中点M，已知△ABC面积为4，求矩形DEFG的面积；

(3) 如图3，扇形OAB中，∠AOB= $\text{[math]}$ ，OA=2. 以点O为原点，OA，OB所在直线为坐标轴建立平面直角坐标系，点P是 $\text{[math]}$ 一动点，点Q是直线y=3上一动点，当△OPQ是和合三角形时，求点P坐标.

综合题困难

3. 如图，在矩形ABCD中，E为AB边上一点，EC平分∠DEB，F为CE的中点，连接AF，BF，过点E作EH∥BC分别交AF，CD于G，H两点．

(1) 求证：DE=DC；

(2) 求证：AF⊥BF；

(3) 当AF•GF=28时，请直接写出CE的长．

综合题困难