1.
定义:在三角形中,把一边的中点到这条边的高线的距离叫做这条边的中垂距.
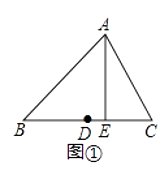
例:如图①,在△ABC中,D为边BC的中点,AE⊥BC于E,则线段DE的长叫做边BC的中垂距.
(1)
设三角形一边的中垂距为d(d≥0).若d=0,则这样的三角形一定是,推断的数学依据是.
(2)
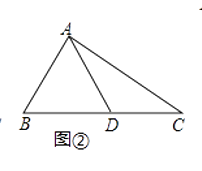
如图②,在△ABC中,∠B=45°,AB=  ,BC=8,AD为边BC的中线,求边BC的中垂距.
(3)
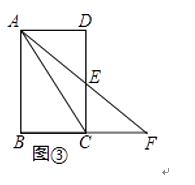
如图③,在矩形ABCD中,AB=6,AD=4.点E为边CD的中点,连结AE并延长交BC的延长线于点F,连结AC.求△ACF中边AF的中垂距.
,BC=8,AD为边BC的中线,求边BC的中垂距.
(3)
如图③,在矩形ABCD中,AB=6,AD=4.点E为边CD的中点,连结AE并延长交BC的延长线于点F,连结AC.求△ACF中边AF的中垂距.
【考点】
全等三角形的判定与性质;
勾股定理;
矩形的性质;
相似三角形的判定与性质;
能力提升
真题演练