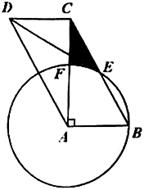
如图，在Rt△ABC中，∠ACB=90°，AC= ，BC=3，△DEF是边长为a（a为小于3的常数）的等边三角形，将△DEF沿AC方向平移，使点D在线段AC上，DE∥AB，设△DEF与△ABC重叠部分的周长为T．

0 返回出卷网首页

1. 如图，在Rt△ABC中，∠ACB=90°，AC= $\text{[math]}$ ，BC=3，△DEF是边长为a（a为小于3的常数）的等边三角形，将△DEF沿AC方向平移，使点D在线段AC上，DE∥AB，设△DEF与△ABC重叠部分的周长为T．

(1) 求证：点E到AC的距离为一个常数；

(2) 若AD= $\text{[math]}$ ，当a=2时，求T的值；

(3) 若点D运动到AC的中点处，请用含a的代数式表示T．

【考点】

等边三角形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 已知△ABC，以AC为边在△ABC外作等腰△ACD，其中AC=AD．

(1) 如图1，若∠DAC=2∠ABC，AC=BC，四边形ABCD是平行四边形，则∠ABC=；

(2) 如图2，若∠ABC=30°，△ACD是等边三角形，AB=3，BC=4．求BD的长；

(3) 如图3，若∠ABC=30°，∠ACD=45°，AC=2，B、D之间距离是否有最大值？如有求出最大值；若不存在，说明理由．

综合题困难

2. 已知：在平面直角坐标系中，抛物线 $\text{[math]}$ 交x轴于A、B两点，交y轴于点C，且对称轴为x=﹣2，点P（0，t）是y轴上的一个动点．

(1) 求抛物线的解析式及顶点D的坐标．

(2) 如图1，当0≤t≤4时，设△PAD的面积为S，求出S与t之间的函数关系式；S是否有最小值？如果有，求出S的最小值和此时t的值．

(3) 如图2，当点P运动到使∠PDA=90°时，Rt△ADP与Rt△AOC是否相似？若相似，求出点P的坐标；若不相似，说明理由．

综合题困难

3. 某公司计划从甲、乙两种产品中选择一种生产并销售，每年产销x件．已知产销两种产品的有关信息如表：

产品	每件售价（万元）	每件成本（万元）	每年其他费用（万元）	每年最大产销量（件）
甲	6	a	20	200
乙	20	10	40+0.05x²	80

其中a为常数，且3≤a≤5

(1) 若产销甲、乙两种产品的年利润分别为y₁万元、y₂万元，直接写出y₁、y₂与x的函数关系式；

(2) 分别求出产销两种产品的最大年利润；

(3) 为获得最大年利润，该公司应该选择产销哪种产品？请说明理由．

综合题普通