1.
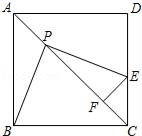
已知边长为1的正方形ABCD中, P是对角线AC上的一个动点(与点A、C不重合),过点P作PE⊥PB ,PE交射线DC于点E,过点E作EF⊥AC,垂足为点F.
(1)
当点E落在线段CD上时(如图),
(2)
当点E落在线段DC的延长线上时,在备用图上画出符合要求的大致图形,并判断上述(1)中的结论是否仍然成立(只需写出结论,不需要证明);
(3)
在点P的运动过程中,△PEC能否为等腰三角形?如果能,试求出AP的长,如果不能,试说明理由.
①求证:PB=PE;
②在点P的运动过程中,PF的长度是否发生变化?若不变,试求出这个不变的值,若变化,试说明理由;
【考点】
三角形内角和定理;
全等三角形的判定与性质;
等腰三角形的性质;
正方形的性质;