1.
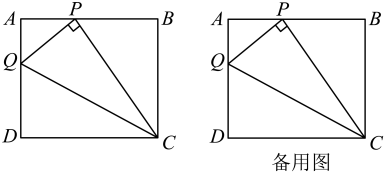
如图1,在矩形  中,
中,  ,动点P,Q分别从C点,A点同时以每秒1个单位长度的速度出发,且分别在边
,动点P,Q分别从C点,A点同时以每秒1个单位长度的速度出发,且分别在边  上沿
上沿  ,
,  的方向运动,当点Q运动到点
的方向运动,当点Q运动到点  时,
时,  两点同时停止运动,设点P运动的时间为
两点同时停止运动,设点P运动的时间为  ,连接
,连接  ,过点P作
,过点P作  ,
,  与边
与边  相交于点E,连接
相交于点E,连接  .
.
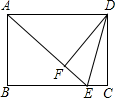
(1)
如图2,当  时,延长
时,延长  交边
交边  于点F.求证:
于点F.求证:  ;
(2)
在(1)的条件下,试探究线段
;
(2)
在(1)的条件下,试探究线段  三者之间的等量关系,并加以证明;
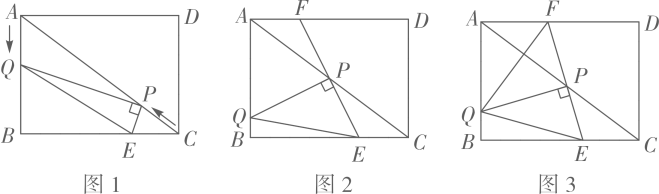
(3)
如图3,当
三者之间的等量关系,并加以证明;
(3)
如图3,当  时,延长
时,延长  交边
交边  于点
于点  ,连接
,连接  ,若
,若  平分
平分  ,求
,求  的值.
的值.
【考点】
勾股定理;
矩形的性质;
两条直线被一组平行线所截,所得的对应线段成比例;
锐角三角函数的定义;
三角形全等的判定-AAS;