1.
如图，在Rt△ABC中，∠ACB＝90°，D为AB边上的一点，以AD为直径的⊙O交BC于点E ， 交AC于点F ， 过点C作CG⊥AB交AB于点G ， 交AE于点H ， 过点E的弦EP交AB于点Q（EP不是直径），点Q为弦EP的中点，连结BP ， BP恰好为⊙O的切线．
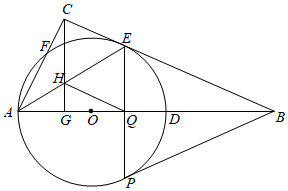
(1)
求证：BC是⊙O的切线．
(2)
求证： 
＝ 
．
(3)
若sin∠ABC═ 
，AC＝15，求四边形CHQE的面积．
【考点】
平行线的性质;
勾股定理;
垂径定理;
圆心角、弧、弦的关系;
切线的判定与性质;
