0 返回出卷网首页
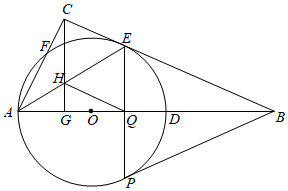
1. 如图，已知⊙O的直径AB=12，弦AC=10，D是 的中点，过点D作DE⊥AC，交AC的延长线于点E.

(1) 求证：DE是⊙O的切线；
(2) 求AE的长.
【考点】
勾股定理; 垂径定理; 切线的判定与性质;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 困难
能力提升
真题演练
换一批
1. 如图，已知AB是⊙O的直径，过O点作OP⊥AB，交弦AC于点D，交⊙O于点E，且使∠PCA=∠ABC．

(1) 求证：PC是⊙O的切线；
(2) 若∠P=60°，PC=2，求PE的长．
综合题 普通
2. 如图所示，以△ABC的边AB为直径作⊙O，点C在⊙O上，BD是⊙O的弦，∠A=∠CBD，过点C作CF⊥AB于点F，交BD于点G，过C作CE∥BD交AB的延长线于点E．


(1) 求证：CE是⊙O的切线；
(2) 求证：CG=BG；
(3) 若∠DBA=30°，CG=4，求BE的长．
综合题 普通
3. 如图，△ABE是⊙O的内接三角形，AB为直径，过点B的切线与AE的延长线交于点C，D是BC的中点，连接DE，连接CO，线段CO的延长线交⊙O于F，FG⊥AB于G．

(1) 求证：DE是⊙O的切线；
(2) 若AE=4，BE=2，求AG的长．
综合题 困难