1.
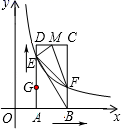
如图,在平面直角坐标系第一象限中,已知点A坐标为(1,0),点D坐标为(1,3),点G坐标为(1,1),动点E从点G出发,以每秒1个单位长度的速度匀速向点D方向运动,与此同时,x轴上动点B从点A出发,以相同的速度向右运动,两动点运动时间为t(0<t<2),以AD、AB分别为边作矩形ABCD , 过点E作双曲线交线段BC于点F , 作CD中点M , 连接BE、EF、EM、FM .
(1)
当t=1时,求点F的坐标.
(2)
若BE平分∠AEF , 则t的值为多少?
(3)
若∠EMF为直角,则t的值为多少?
【考点】
待定系数法求反比例函数解析式;
等腰三角形的性质;
勾股定理;
反比例函数图象上点的坐标特征;
能力提升

