0 返回出卷网首页
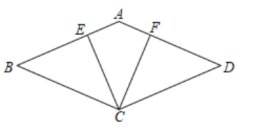
1. 如图，在菱形ABCD中，点E、F分别在BC，CD上，且CE=CF。

(1) 求证：△ABE≌△ADF.
(2) 若∠BAE=∠EAF=40°，求∠AEB的度数。
【考点】
菱形的性质; 三角形全等的判定-SAS;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 如图，已知菱形ABCD中，分别以C、D为圆心，大于 CD的长为半径作弧，两弧分别相交于M、N两点，直线MN交CD于点F ， 交对角线AC于点E ， 连接BE、DE ．

(1) 求证：BE＝CE；
(2) 若∠ABC＝72°，求∠ABE的度数．
综合题 普通
2. 如图，四边形ABCD为菱形，E为对角线AC上的一个动点（不与点A，C重合），连接DE并延长交射线AB于点F，连接BE．

(1) 求证：；
(2) 求证： ．
综合题 普通
3. 如图，在菱形ABCD中，对角线AC与BD相交于点O，AB=8，∠BAD=60°，点E从点A出发，沿AB以每秒2个单位长度的速度向终点B运动，当点E不与点A重合时，过点E作EF⊥AD于点F，作EG∥AD交AC于点G，过点G作GH⊥AD交AD（或AD的延长线）于点H，得到矩形EFHG，设点E运动的时间为t秒

(1) 求线段EF的长（用含t的代数式表示）；
(2) 求点H与点D重合时t的值；
(3) 设矩形EFHG与菱形ABCD重叠部分图形的面积与S平方单位，求S与t之间的函数关系式；
(4) 矩形EFHG的对角线EH与FG相交于点O′，当OO′∥AD时，t的值为；当OO′⊥AD时，t的值为．
综合题 困难