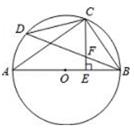
1.
 内接于
内接于  边于点
边于点  ,连接
,连接  .
.
(1)
如图1,求证:  ;
(2)
如图2,延长
;
(2)
如图2,延长  交
交  于点
于点  ,点
,点  在线段
在线段  上,射线
上,射线  交
交  边于点
边于点  ,连接
,连接  ,若
,若  ,求证:
,求证:  ;
(3)
如图3,在
;
(3)
如图3,在  的条件下,连接
的条件下,连接  ,若
,若  ,
,  ,求线段
,求线段  的长.
的长.



【考点】
三角形内角和定理;
等腰三角形的性质;
勾股定理;
圆周角定理;
圆的综合题;
能力提升