1.
某数学活动小组在一次活动中，对一个数学问题做了如下研究：
(1)
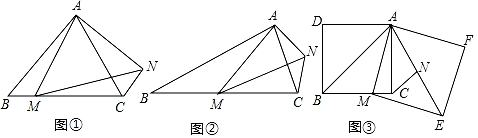
（问题发现）如图①，在等边三角形ABC中，点M是BC边上任意一点，连接AM，以AM为边作等边三角形AMN，连接CN，则∠ABC和∠ACN的数量关系为；
(2)
（变式探究）如图②，在等腰三角形ABC中，AB＝BC，点M是BC边上任意一点（不含端点B，C，连接AM，以AM为边作等腰三角形AMN，使∠AMN＝∠ABC，AM＝MN，连接CN，试探究∠ABC与∠ACN的数量关系，并说明理由；
(3)
（解决问题）如图③，在正方形ADBC中，点M为BC边上一点，以AM为边作正方形AMEF，点N为正方形AMEF的中心，连接CN，AB，AE，若正方形ADBC的边长为8，CN＝ 
，直接写出正方形AMEF的边长.
【考点】
等腰三角形的性质;
等边三角形的性质;
正方形的性质;
相似三角形的判定与性质;
三角形全等的判定-SAS;
能力提升
