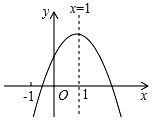1.
我们约定:  为函数
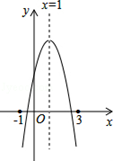
为函数  的关联数,当其图象与坐标轴交点的横、纵坐标均为整数时,该交点为“整交点”,若关联数为
的关联数,当其图象与坐标轴交点的横、纵坐标均为整数时,该交点为“整交点”,若关联数为  的函数图象与x轴有两个整交点(m为正整数),则这个函数图象上整交点的坐标为.
的函数图象与x轴有两个整交点(m为正整数),则这个函数图象上整交点的坐标为.
【考点】
二次函数图象与坐标轴的交点问题;
二次函数图象上点的坐标特征;
基础巩固
能力提升
变式训练
拓展培优
真题演练