1.
中心为O的正六边形  的半径为
的半径为  .点
.点  同时分别从
同时分别从  两点出发,以
两点出发,以  的速度沿
的速度沿  向终点
向终点  运动,连接
运动,连接  ,设运动时间为
,设运动时间为  .
.
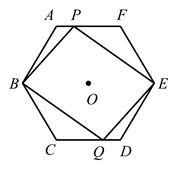
(1)
求证:四边形  为平行四边形;
(2)
求矩形
为平行四边形;
(2)
求矩形  的面积与正六边形
的面积与正六边形  的面积之比.
的面积之比.
【考点】
三角形的面积;
等边三角形的性质;
平行四边形的判定与性质;
相似三角形的判定与性质;
正多边形的性质;
平行四边形的面积;
能力提升