如图，在▱ABCD中，点E、F分别在边AD、BC上，且∠ABE＝∠CDF．

0 返回出卷网首页

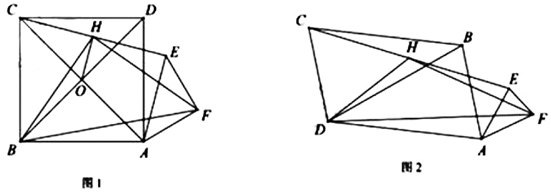
1. 如图，在▱ABCD中，点E、F分别在边AD、BC上，且∠ABE＝∠CDF．

(1) 探究四边形BEDF的形状，并说明理由；

(2) 连接AC，分别交BE、DF于点G、H，连接BD交AC于点O．若 $\text{[math]}$ ， AE＝4，求BC的长．

【考点】

平行四边形的判定与性质; 相似三角形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，在 $\text{[math]}$ 中，过点C作 $\text{[math]}$ ，E是AC的中点，连接DE并延长，交AB于点F，交CB的延长线于点G，连接AD，CF．

(1) 求证：四边形AFCD是平行四边形．

(2) 若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，求AB的长．

综合题普通

2. 如图，在 $\text{[math]}$ 中，D是边 $\text{[math]}$ 的中点，连结 $\text{[math]}$ 并延长至点E，使 $\text{[math]}$ ，延长 $\text{[math]}$ 至点F，使 $\text{[math]}$ ，连结 $\text{[math]}$ 、 $\text{[math]}$ .

(1) 求证：四边形 $\text{[math]}$ 是平行四边形.

(2) 连结 $\text{[math]}$ ，交线段 $\text{[math]}$ 于点G.若 $\text{[math]}$ 的面积为2，则 $\text{[math]}$ 的面积为.

综合题普通

3. 如图，在△ABC中，点D、E、F分别在AB、BC、AC边上，DE∥AC，EF∥AB.

(1) 求证：△BDE∽△EFC；

(2) 若 $\text{[math]}$ ，且S_△DBE＝2，求△ABC的面积.

综合题普通