如图

0 返回出卷网首页

1. 如图

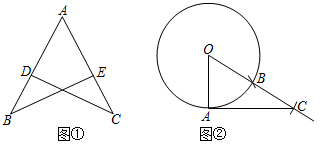
(1) 如图①，点D在AB上，点E在AC上，AD＝AE，∠B＝∠C.求证：AB＝AC.

(2) 如图②，A为⊙O上一点，按以下步骤作图：

①连接OA；

②以点A为圆心，AO长为半径作弧，交⊙O于点B；

③在射线OB上截取BC＝OA；

④连接AC.

若AC＝3，求⊙O的半径.

【考点】

三角形全等及其性质; 等边三角形的判定与性质; 含30°角的直角三角形; 三角形全等的判定-AAS;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，∠1=∠2，AD=AE，∠B=∠ACE，且B、C、D三点在一条直线上，

(1) 试说明△ABD与△ACE全等的理由；

(2) 如果∠B=60°，试说明线段AC、CE、CD之间的数量关系，并说明理由.

综合题普通

2. 如图，在等边三角形ABC中，点D，E分别在边BC，AC上，且DE∥AB，过点E作EF⊥DE，交BC的延长线于点F．

(1) 求∠F的度数；

(2) 若CD=2，求DF的长．

综合题普通

3. 如图，在等边三角形 $\text{[math]}$ 中， $\text{[math]}$ 为 $\text{[math]}$ 边上任意一点，延长 $\text{[math]}$ 至点 $\text{[math]}$ ，使 $\text{[math]}$ ，连结 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ．

(1) 求证： $\text{[math]}$ ；

(2) 若 $\text{[math]}$ ，求线段 $\text{[math]}$ 的长（结果用含 $\text{[math]}$ 的代数式表示）．

综合题普通