1.
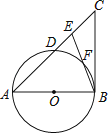
如图,AB是⊙O的直径,点D在直径AB上(D与A,B不重合),CD⊥AB,且CD=AB,连接CB,与⊙O交于点F,在CD上取一点E,使EF=EC.
(1)
求证:EF是⊙O的切线;
(2)
若D是OA的中点,AB=4,求CF的长.
【考点】
等腰三角形的性质;
勾股定理;
切线的判定;
相似三角形的判定与性质;