1.
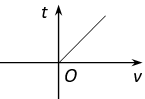
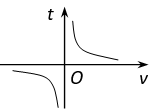
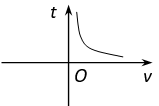
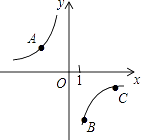
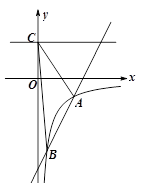
已知电流I(安培)、电压U(伏特)、电阻R(欧姆)之间的关系为  ,当电压为定值时,I关于R的函数图象是( )
,当电压为定值时,I关于R的函数图象是( )
A.
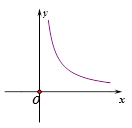 B.
B.
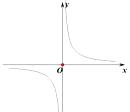 C.
C.
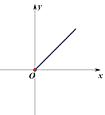 D.
D.
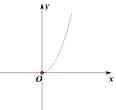
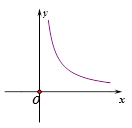 B.
B.
 C.
C.
 D.
D.

【考点】
反比例函数的概念;
反比例函数的图象;
反比例函数的性质;
基础巩固
能力提升
变式训练
拓展培优