1.
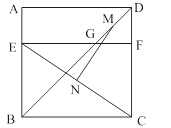
如图,四边形ABCD是边长为6的正方形,点E在边AB上,BE=4,过点E作EF∥BC,分别交BD、CD于G、F两点.若M、N分别是DG、CE的中点,则MN的长为 ( )
A.
3
B.
 C.
C.
 D.
4
D.
4
【考点】
勾股定理;
正方形的性质;
相似三角形的判定与性质;
三角形的中位线定理;