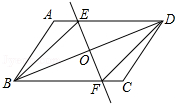
如图，在▱ABCD中，点E、F、G、H分别在边AB、BC、CD、DA上，AE=CG，AH=CF，且EG平分∠HEF．

0 返回出卷网首页

1. 如图，在▱ABCD中，点E、F、G、H分别在边AB、BC、CD、DA上，AE=CG，AH=CF，且EG平分∠HEF．

(1) 求证：△AEH≌△CGF；

(2) 求证：四边形EFGH是菱形．

【考点】

全等三角形的判定与性质; 平行四边形的性质; 菱形的判定;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，在▱ABCD中，E，F分别为边AB，CD的中点，BD是对角线．

(1) 求证：△ADE≌△CBF；

(2) 若∠ADB是直角，请证明四边形BEDF是菱形．

综合题普通

2. 如图，已知：在平行四边形ABCD中，点E、F、G、H分别在边AB、BC、CD、DA上，AE=CG，AH=CF，且EG平分∠HEF．求证：

(1) △AEH≌△CGF；

(2) 四边形EFGH是菱形．

综合题普通

3. 如图，已知平行四边形ABCD，延长AD到E，使DE=AD，连接BE与DC交于O点．

(1) 求证：△BOC≌△EOD；

(2) 当△ABE满足什么条件时，四边形BCED是菱形？证明你的结论．

综合题普通