1.
某研究性学习小组在探究矩形的折纸问题时,将一块直角三角板的直角顶点绕矩形ABCD(AB<BC)的对角线的交点O旋转(①⇒②⇒③),图中的M、N分别为直角三角形的直角边与矩形ABCD的边CD、BC的交点.
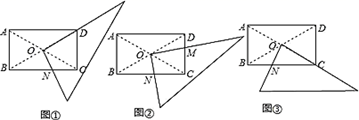
(1)
该学习小组成员意外的发现图①(三角板一直角边与OD重合)中,BN2=CD2+CN2 , 在图③中(三角板一边与OC重合),CN2=BN2+CD2 , 请你对这名成员在图①和图③中发现的结论选择其一说明理由.
(2)
试探究图②中BN、CN、CM、DM这四条线段之间的数量关系,写出你的结论,并说明理由.
(3)
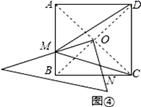
将矩形ABCD改为边长为1的正方形ABCD,直角三角板的直角顶点绕O点旋转到图④,两直角边与AB、BC分别交于M、N,直接写出BN、CN、CM、DM这四条线段之间所满足的数量关系.(不需要证明)
【考点】
三角形全等及其性质;
三角形全等的判定;
勾股定理;
正方形的性质;
能力提升


