在正方形ABCD中，连接AC ，点E在线段AD上，连接BE交AC于M ，过点M作FM⊥BE交CD于F ．

0 返回出卷网首页

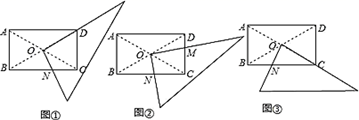
1. 在正方形ABCD中，连接AC ，点E在线段AD上，连接BE交AC于M ，过点M作FM⊥BE交CD于F ．

(1) 如图①，求证：∠ABE+∠CMF＝∠ACD；

(2) 如图②，求证：BM＝MF；

(3) 如图③，连接BF ，若点E为AD的中点，AB＝6，求BF的长．

【考点】

三角形全等及其性质; 三角形全等的判定; 勾股定理; 正方形的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 某研究性学习小组在探究矩形的折纸问题时，将一块直角三角板的直角顶点绕矩形ABCD(AB＜BC)的对角线的交点O旋转(①⇒②⇒③)，图中的M、N分别为直角三角形的直角边与矩形ABCD的边CD、BC的交点．

(1) 该学习小组成员意外的发现图①(三角板一直角边与OD重合)中，BN²=CD²+CN² ，在图③中(三角板一边与OC重合)，CN²=BN²+CD² ，请你对这名成员在图①和图③中发现的结论选择其一说明理由．

(2) 试探究图②中BN、CN、CM、DM这四条线段之间的数量关系，写出你的结论，并说明理由．

(3) 将矩形ABCD改为边长为1的正方形ABCD，直角三角板的直角顶点绕O点旋转到图④，两直角边与AB、BC分别交于M、N，直接写出BN、CN、CM、DM这四条线段之间所满足的数量关系．(不需要证明)

综合题困难

2. 如图1， $\text{[math]}$ 的顶点在正方形ABCD两条对角线的交点处， $\text{[math]}$ ，将 $\text{[math]}$ 绕点P旋转，旋转过程中， $\text{[math]}$ 的两边分别与正方形ABCD的边AD和CD交于点E ， F（点F与点C ， D不重合）。探索线段DE ， DF ， AD之间的数量关系．

(1) 爱动脑筋的小悦发现，通过证明两个三角形全等，可以得到结论．请你写出线段DE ， DF ， AD之间的数量关系，并说明理由；

(2) 如图2，将图13中的正方形ABCD改为 $\text{[math]}$ 的菱形， $\text{[math]}$ ，其他条件不变，请你帮小悦得出此时线段DE ， DF ， AD之间的数量关系是；

(3) 如图3，在（2）的条件下，当菱形的边长为8，点P运动至与A点距离恰好为7的位置，且 $\text{[math]}$ 旋转至 $\text{[math]}$ 时，DE的长度为．

综合题困难

3. 如图，在正方形ABCD中，AB＝6，M是CD边上一动点（不与D点重合），点D与点E关于AM所在的直线对称，连接AE，ME，延长CB到点F，使得BF＝DM，连接EF，AF．

(1) 当DM＝2时，依题意补全图1；

(2) 在（1）的条件下，求线段EF的长；

(3) 当点M在CD边上运动时，能使△AEF为等腰三角形，请直接写出此时DM与AD的数量关系．

综合题困难