如图，AD是△ABC的中线，AE∥BC ， BE交AD于点F ， F是AD的中点，连接EC ．

0 返回出卷网首页

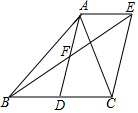
1. 如图，AD是△ABC的中线，AE∥BC ， BE交AD于点F ， F是AD的中点，连接EC ．

(1) 求证：四边形ADCE是平行四边形；

(2) 若四边形ABCE的面积为S ，请直接写出图中所有面积是 $\text{[math]}$ S的三角形．

【考点】

三角形的面积; 平行四边形的判定;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 正方形网格中的每个小正方形边长都是1，

(1) 请在图中画出等腰△ABC ，使AB＝AC＝ $\text{[math]}$ ，BC＝ $\text{[math]}$ ；

(2) 在△ABC中，AB边上的高为．

综合题普通

2. 如图，边长为1的正方形组成的网格中，△AOB的顶点均在格点上，点A、B的坐标分别是A（3，2），B（1，3）．

(1) 写出△AOB的面积为；

(2) 点P在x轴上，当PA+PB的值最小时，在图中画出点P，并直接写出PA+PB的最小值为．

综合题普通

3. 设一个三角形的三边分别为a ， b ， c ， p= $\text{[math]}$ （a+b+c），则有下列面积公式：S= $\text{[math]}$ （海伦公式）；S= $\text{[math]}$ （秦九韶公式）．

(1) 一个三角形的三边长依次为3，5，6，任选以上一个公式求这个三角形的面积；

(2) 一个三角形的三边长依次为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，任选以上一个公式求这个三角形的面积．

综合题普通