如图1，△ABC中，点D，E，F分别在边AB，BC，AC上，BE=CE，点G在线段CD上，CG=CA，GF=DE，∠AFG=∠CDE。

0 返回出卷网首页

1. 如图1，△ABC中，点D，E，F分别在边AB，BC，AC上，BE=CE，点G在线段CD上，CG=CA，GF=DE，∠AFG=∠CDE。

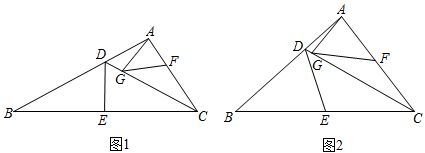
(1) 填空：与∠CAG相等的角是。

(2) 用等式表示线段AD与BD的数量关系，并证明；

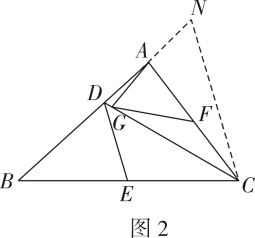
(3) 若∠BAC=90°，∠ABC=2∠ACD(如图2)，求 $\text{[math]}$ 的值。

【考点】

等腰三角形的判定与性质; 平行四边形的判定与性质; 三角形全等的判定-SAS; 三角形的中位线定理;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图， $\text{[math]}$ 中，D、E分别为边 $\text{[math]}$ 、 $\text{[math]}$ 中点，连接 $\text{[math]}$ 并延长至点F，使得 $\text{[math]}$ ，连接 $\text{[math]}$ .

(1) 求证： $\text{[math]}$ ；

(2) 若 $\text{[math]}$ ， $\text{[math]}$ ，求四边形 $\text{[math]}$ 的周长.

综合题普通

2. 已知，如图，在平行四边形ABCD中，点G，H分别是AB，CD的中点，点E，F在对角线AC上，且AE=CF．

(1) 求证：四边形EGFH是平行四边形．

(2) 连结BD交AC于点O，若BD=12，AE=EF-CF，求EG的长．

综合题普通

3. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 的平分线 $\text{[math]}$ 分别与线段 $\text{[math]}$ 交于点F，E， $\text{[math]}$ 与 $\text{[math]}$ 交于点G.

(1) 求证： $\text{[math]}$ .

(2) 若 $\text{[math]}$ ，求 $\text{[math]}$ 的长度.

综合题普通