1.
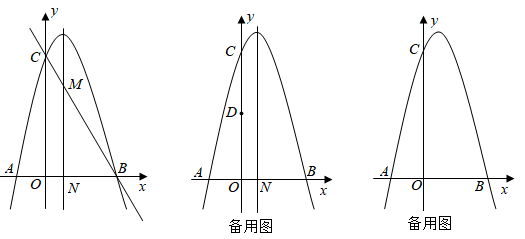
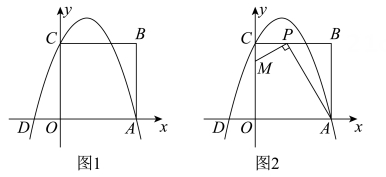
如图1,在平面直角坐标系中,抛物线与x轴交于点 A(-1,0) ,B(点A在点B的左侧),交y轴与点(0,-3),抛物线的对称轴为直线x=1,点D为抛物线的顶点.


(1)
求该抛物线的解析式;
(2)
已知经过点A的直线y=kx+b(k>0)与抛物线在第一象限交于点E,连接AD,DE,BE,当  时,求点E的坐标.
(3)
如图2,在(2)中直线AE与y轴交于点F,将点F向下平移
时,求点E的坐标.
(3)
如图2,在(2)中直线AE与y轴交于点F,将点F向下平移  个单位长度得到Q,连接QB.将△OQB绕点O逆时针旋转一定的角度
个单位长度得到Q,连接QB.将△OQB绕点O逆时针旋转一定的角度  (0°<
(0°<  <360°)得到
<360°)得到  ,直线
,直线  与x轴交于点G.问在旋转过程中是否存在某个位置使得
与x轴交于点G.问在旋转过程中是否存在某个位置使得  是等腰三角形?若存在,请直接写出所有满足条件的点
是等腰三角形?若存在,请直接写出所有满足条件的点  的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【考点】
二次函数-动态几何问题;
真题演练