1.
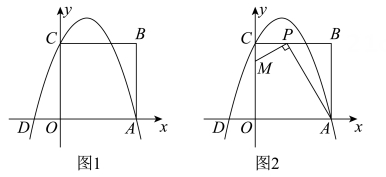
如图1,已知在平面直角坐标系xOy中,四边形OABC是边长为3的正方形,其中顶点A,C分别在x轴的正半轴和y轴的正半轴上.抛物线y=-x2+bx+c经过A,C两点,与x轴交于另一个点D.
(1)
①求点A,B,C的坐标;
(2)
若点P是边BC上的一个动点,连结AP,过点P作PM⊥AP,交y轴于点M(如图2所示).当点P在BC上运动时,点M也随之运动.设BP=m,CM=n,试用含m的代数式表示n,并求出n的最大值.
②求b,c的值.
【考点】
二次函数的最值;
正方形的性质;
相似三角形的判定与性质;
二次函数-动态几何问题;
能力提升
1.
如图,点E是正方形ABCD的边BC延长线上一点,联结DE,过顶点B作BF⊥DE,垂足为F,BF交边DC于点G.

(1)
求证:GD•AB=DF•BG;
(2)
联结CF,求证:∠CFB=45°.

