1.
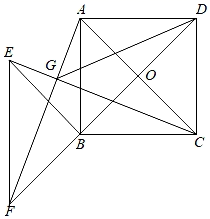
如图,在正方形ABCD中,对角线AC与BD相交于点O,以B为顶点的等腰Rt△BEF绕点B旋转,连接AF与CE相交于点G,连接DG.
(1)
求证:CE⊥AF;
(2)
求证:AG+CG=  DG;
(3)
连接CF,当EG∶AG∶FG=l∶2∶5,且S正方形ABCD=100时,求DG的长和△BCF的面积.
DG;
(3)
连接CF,当EG∶AG∶FG=l∶2∶5,且S正方形ABCD=100时,求DG的长和△BCF的面积.
【考点】
三角形全等及其性质;
勾股定理;
四边形的综合;
能力提升