如图1，将三角板放在正方形ABCD上，使三角板的直角顶点E与正方形ABCD的顶点A重合，三角扳的一边交CD于点F，另一边交CB的延长线于点G，

0 返回出卷网首页

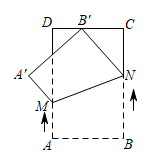
1. 如图1，将三角板放在正方形ABCD上，使三角板的直角顶点E与正方形ABCD的顶点A重合，三角扳的一边交CD于点F，另一边交CB的延长线于点G，

(1) 求证：EF=EG；

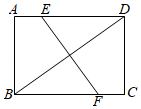
(2) 如图2，移动三角板，使顶点E始终在正方形ABCD的对角线AC上，其他条件不变，（1）中的结论是否仍然成立？若成立，请给予证明：若不成立．请说明理由：

(3) 如图3，将（2）中的“正方形ABCD”改为“矩形ABCD”，且使三角板的一边经过点B，其他条件不变，若AB=a、BC=b，求 $\text{[math]}$ 的值．

【考点】

矩形的性质; 相似三角形的判定与性质; 三角形全等的判定-ASA;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，已知点P在矩形ABCD外，∠APB=90°，PA=PB，点E，F分别在AD，BC上运动，且∠EPF=45°，连接EF．

(1) 求证：△APE∽△BFP；

(2) 当∠PEF=90°，AE=2时，

①求AB的长；

②直接写出EF的长；

(3) 直接写出线段AE、BF、EF之间的数量关系．

综合题普通

2. 综合与实践﹣四边形旋转中的数学

“智慧”数学小组在课外数学活动中研究了一个问题，请帮他们解答．

任务一：如图1，在矩形ABCD中，AB=6，AD=8，E，F分别为AB，AD边的中点，四边形AEGF为矩形，连接CG．

(1) 请直接写出CG的长是．

(2) 如图2，当矩形AEGF绕点A旋转（比如顺时针旋转）至点G落在边AB上时，请计算DF与CG的长，通过计算，试猜想DF与CG之间的数量关系．

(3) 当矩形AEGF绕点A旋转至如图3的位置时，（2）中DF与CG之间的数量关系是否还成立？请说明理由．

任务二：“智慧”数学小组对图形的旋转进行了拓展研究，如图4，在▱ABCD中，∠B=60°，AB=6，AD=8，E，F分别为AB，AD边的中点，四边形AEGF为平行四边形，连接CG．“智慧”数学小组发现DF与CG仍然存在着特定的数量关系．

(4) 如图5，当▱AEGF绕点A旋转（比如顺时针旋转），其他条件不变时，“智慧”数学小组发现DF与CG仍然存在着这一特定的数量关系．请你直接写出这个特定的数量关系．

综合题困难

3. 如图，在平面直角坐标系 $\text{[math]}$ 中，矩形 $\text{[math]}$ 的边 $\text{[math]}$ ， $\text{[math]}$ 分别在 $\text{[math]}$ 轴， $\text{[math]}$ 轴上，且点 $\text{[math]}$ 的坐标为 $\text{[math]}$ . $\text{[math]}$ 是边 $\text{[math]}$ 上的动点，以 $\text{[math]}$ 为一边在其右侧作矩形 $\text{[math]}$ ，其中 $\text{[math]}$ ，连结 $\text{[math]}$ ， $\text{[math]}$ .

(1) 证明： $\text{[math]}$ ；

(2) 当点 $\text{[math]}$ 点坐标为 $\text{[math]}$ 时，求点 $\text{[math]}$ 的坐标；

(3) 证明点 $\text{[math]}$ 的运动范围是一条线段，并求该线段的长.

综合题困难