1.
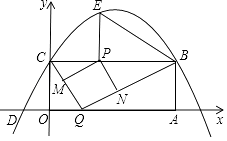
如图,矩形OABC的两边在坐标轴上,点A的坐标为(10,0),抛物线y=ax2+bx+4过点B,C两点,且与x轴的一个交点为D(﹣2,0),点P是线段CB上的动点,设CP=t(0<t<10).
(1)
请直接写出B、C两点的坐标及抛物线的解析式;
(2)
过点P作PE⊥BC,交抛物线于点E,连接BE,当t为何值时,∠PBE=∠OCD?
(3)
点Q是x轴上的动点,过点P作PM∥BQ,交CQ于点M,作PN∥CQ,交BQ于点N,当四边形PMQN为正方形时,请求出t的值.
【考点】
待定系数法求二次函数解析式;
矩形的性质;
相似三角形的性质;


