如图，将△ABC绕点C顺时针旋转得到△DEC，使点A的对应点D恰好落在边AB上，点B的对应点为E，连接BE．

0 返回出卷网首页

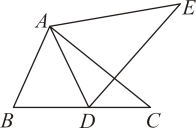
1. 如图，将△ABC绕点C顺时针旋转得到△DEC，使点A的对应点D恰好落在边AB上，点B的对应点为E，连接BE．

(1) 求证：∠A＝∠EBC；

(2) 若已知旋转角为50°，∠ACE＝130°，求∠CED和∠BDE的度数．

【考点】

三角形内角和定理; 等腰三角形的性质; 旋转的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 在同一平面内，将 $\text{[math]}$ 绕点A逆时针方向旋转到 $\text{[math]}$ 的位置，使得 $\text{[math]}$ ，连接 $\text{[math]}$ ，则 $\text{[math]}$ 的度数？

解答题普通

2. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，将 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转后得到 $\text{[math]}$ ， C点落在 $\text{[math]}$ 边上，若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数．

解答题普通

3. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，将 $\text{[math]}$ 绕点B逆时针旋转得到 $\text{[math]}$ ，点C，A的对应点分别为点E，F，点E落在 $\text{[math]}$ 上，连接 $\text{[math]}$ ．若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数．

解答题普通