如图，在平面直角坐标系中，把矩形OABC沿对角线AC所在直线折叠，点B落在点D处，DC与y轴相交于点E，矩形OABC的边OC，OA的长是关于x的一元二次方程x2﹣12x+32=0的两个根，且OA＞OC．

0 返回出卷网首页

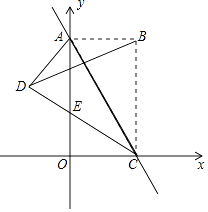
1. 如图，在平面直角坐标系中，把矩形OABC沿对角线AC所在直线折叠，点B落在点D处，DC与y轴相交于点E，矩形OABC的边OC，OA的长是关于x的一元二次方程x²﹣12x+32=0的两个根，且OA＞OC．

(1) 求线段OA，OC的长；

(2) 求证：△ADE≌△COE，并求出线段OE的长；

(3) 直接写出点D的坐标；

(4) 若F是直线AC上一个动点，在坐标平面内是否存在点P，使以点E，C，P，F为顶点的四边形是菱形？若存在，请直接写出P点的坐标；若不存在，请说明理由．

【考点】

全等三角形的应用; 菱形的性质; 相似三角形的应用;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 在正方形ABCD中，对角线AC、BD交于点O，动点P在线段BC上（不含点B），∠BPE= $\text{[math]}$ ∠ACB，PE交BO于点E，过点B作BF⊥PE，垂足为F，交AC于点G．

(1) 当点P与点C重合时（如图①），求证：△BOG≌△POE；

(2) 通过观察、测量、猜想： $\text{[math]}$ =，并结合图②证明你的猜想；

(3) 把正方形ABCD改为菱形，其他条件不变（如图③），若∠ACB=α，求 $\text{[math]}$ 的值．（用含α的式子表示）

综合题困难

2. 如图，在平面直角坐标系中，四边形ABCO为正方形，A点坐标为（0，2），点P为x轴负半轴上一动点，以AP为直角作等腰直角三角形APD，∠APD=90°（点D落在第四象限）

(1) 当点P的坐标为（﹣1，0）时，求点D的坐标；

(2) 点P在移动的过程中，点D是否在直线y=x﹣2上？请说明理由；

(3) 连接OB交AD于点G，求证：AG=DG．

综合题困难

3. 如图1，在四边形ABCD中，AD∥BC，DB=DC=EC，∠A=2∠ADB，AD=m，AB=n．

(1) 在图1中找出与∠ABD相等的角，并加以证明；

(2) 求BE的长；

(3) 将△ABD沿BD翻折，得到△A′BD．若点A′恰好落在EC上（如图2），求 $\text{[math]}$ 的值．

综合题普通