如图，凸四边形ABCD中，AD＝BD，AD⊥BD.

0 返回出卷网首页

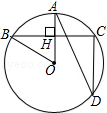
1. 如图，凸四边形ABCD中，AD＝BD，AD⊥BD.

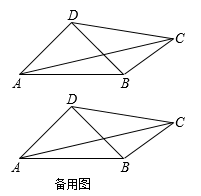
(1) 若BC//AD，以顶点D为圆心，DA的长为半径作圆，请指出⊙D与直线BC的位置关系，并说明理由；

(2) 当AB＝2 $\text{[math]}$ ，∠BCD＝30°时，求四边形ABCD的面积的最大值；

(3) 若BC＝1，CD＝2，AC＝3，求∠BCD的度数.

【考点】

三角形全等及其性质; 勾股定理; 垂径定理; 圆周角定理; 直线与圆的位置关系;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 已知， $\text{[math]}$ 是 $\text{[math]}$ 直径，弦 $\text{[math]}$ 于点 $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 上一点．

(1) 如图1，连接 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ，求证： $\text{[math]}$ 平分 $\text{[math]}$ ；

(2) 如图2，连接 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ， $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，若 $\text{[math]}$ ；求证： $\text{[math]}$ ；

(3) 如图 $\text{[math]}$ ，在（2）的条件下，连接 $\text{[math]}$ 交 $\text{[math]}$ 于 $\text{[math]}$ ，连接 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 半径．

综合题困难

2. 如图，△ABC内接于⊙O，AB是⊙O的直径，AB=10，AC=6. 连接OC，弦AD分别交OC，BC于点E，F，其中E是AD的中点.

(1) 求证：∠CAD=∠CBA.

(2) 求OE的长.

综合题普通

3. 如图，在⊙O中，半径OA⊥弦BC于点H，点D在优弧BC上

(1) 若∠AOB=50°，求∠ADC的度数；

(2) 若BC=8，AH=2，求⊙O的半径.

综合题普通