1.
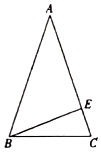
为迎接十四运,我区强力推进“三改一通一落地”,加速城市更新步伐,绿地广场有一块三角形空地将进行绿化,如图,在△ABC中,AB=AC,E是AC上的一点,CE=5,BC=13,BE=12.
(1)
判断△ABE的形状,并说明理由;
(2)
求线段AB的长.
【考点】
勾股定理;
勾股定理的逆定理;