如图，已知：抛物线y＝x2+bx+c与直线l交于点A（﹣1，0），C（2，﹣3），与x轴另一交点为B.

0 返回出卷网首页

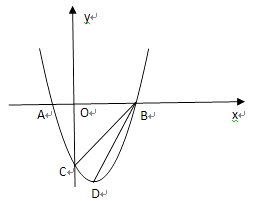
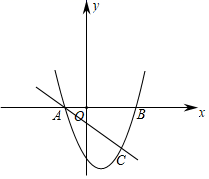
1. 如图，已知：抛物线y＝x²+bx+c与直线l交于点A（﹣1，0），C（2，﹣3），与x轴另一交点为B.

(1) 求抛物线的解析式；

(2) 在抛物线上找一点P，使△ACP的内心在x轴上，求点P的坐标；

(3) M是抛物线上一动点，过点M作x轴的垂线，垂足为N，连接BM.在（2）的条件下，是否存在点M，使∠MBN＝∠APC？若存在，请求出点M的坐标；若不存在，请说明理由.

【考点】

待定系数法求二次函数解析式; 勾股定理; 勾股定理的逆定理; 锐角三角函数的定义; 二次函数与一次函数的综合应用;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于 $\text{[math]}$ ， $\text{[math]}$ 两点，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ．

(1) 求抛物线的解析式；

(2) 如图 $\text{[math]}$ ，点 $\text{[math]}$ 是直线 $\text{[math]}$ 上方抛物线上的动点，过点 $\text{[math]}$ 作 $\text{[math]}$ 轴交直线 $\text{[math]}$ 于点 $\text{[math]}$ ，作 $\text{[math]}$ 轴交直线 $\text{[math]}$ 于点 $\text{[math]}$ ，求 $\text{[math]}$ ， $\text{[math]}$ 两点间距离的最大值；

(3) 如图 $\text{[math]}$ ，连接 $\text{[math]}$ ，在抛物线上求出点 $\text{[math]}$ ，使 $\text{[math]}$ ．

综合题困难

2. 已知：在平面直角坐标系xOy中，对称轴为直线x = -2的抛物线经过点C(0，2)，与x轴交于A(-3，0)、B两点(点A在点B的左侧).

(1) 求这条抛物线的表达式.

(2) 连接BC，求∠BCO的余切值.

(3) 如果过点C的直线，交x轴于点E，交抛物线于点P，且∠CEO =∠BCO，求点P的坐标.

综合题困难

3. 如图：抛物线与x轴交于A（－1，0）、B（3，0）两点，与y轴交于点C，OB=OC，连接BC，抛物线的顶点为D．连结B、D两点．

(1) 求抛物线的解析式．

(2) 求∠CBD的正弦值．

综合题普通