0 返回出卷网首页
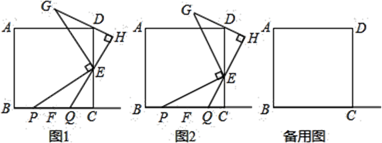
1. 如图1，放置的一副三角尺，将含45°角的三角尺斜边中点O为旋转中心，逆时针旋转30°得到如图2，连接OB、OD、AD．

(1) 求证：△AOB≌△AOD；
(2) 试判定四边形ABOD是什么四边形，并说明理由．
【考点】
全等三角形的判定与性质; 旋转的性质;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 如图，△OAB在平面直角坐标系中，∠BAO=90°，将△OAB绕点O顺时针旋转，使点B落在点D处，得到△ODE，过点B作平行于x轴的直线交OE于点F，交y轴于点N，直线FM交OB于点M。S△OAB=16，tan∠DOE= 。

(1) 求经过点M、F的反比例函数）y1= 和直线FM：y2=k2x+b的解析式；
(2) 过点Ｍ作MH⊥x轴，求五边形NFMHO的面积；
(3) 直接写出当 >k2x+b时x的值。
综合题 普通
2. 如图①，在△ABC中，∠ACB=90°，AC=BC，∠EAC=90°，点M为射线AE上任意一点（不与点A重合），连接CM，将线段CM绕点C按顺时针方向旋转90°得到线段CN，直线NB分别交直线CM，射线AE于点F、D．

(1) 问题发现：直接写出∠NDE=度；
(2) 拓展探究：试判断，如图②当∠EAC为钝角时，其他条件不变，∠NDE的大小有无变化？请给出证明．
(3) 如图③，若∠EAC=15°，BD= ，直线CM与AB交于点G，其他条件不变，请直接写出AC的长．
综合题 困难
3. 如图1：已知△ABC中，∠BAC=90°，AB=AC，在∠BAC内部作∠MAN=45°．AM、AN分别交BC于点M，N．

(1) 将△ABM绕点A逆时针旋转90°，使AB边与AC边重合，把旋转后点M的对应点记作点Q，得到ACQ，请在图1中画出△ACQ；（不写出画法）
(2) 在（1）中作图的基础上，连接NQ，

①求证“MN=NQ”；

②写出线段BM，MN和NC之间满足的数量关系，并简要说明理由．
(3) 线段GS，ST和TH之间满足的数量关系是
(4) 设DK=a，DE=b，求DP的值．（用a，b表示）
综合题 普通