如图，AB是⊙O的直径，弦CD与AB交于点E，过点B的切线BP与CD的延长线交于点P，连接OC，CB．

0 返回出卷网首页

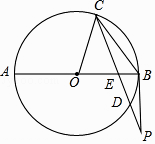
1. 如图，AB是⊙O的直径，弦CD与AB交于点E，过点B的切线BP与CD的延长线交于点P，连接OC，CB．

(1) 求证：AE•EB=CE•ED；

(2) 若⊙O的半径为3，OE=2BE， $\text{[math]}$ = $\text{[math]}$ ，求tan∠OBC的值及DP的长．

【考点】

切线的性质; 相似三角形的判定与性质; 解直角三角形;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，从 $\text{[math]}$ 外一点 $\text{[math]}$ 引割线 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 相切于点 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .

(1) 求证： $\text{[math]}$ ；

(2) 已知 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长.

综合题普通

2. 如图，AB是 $\text{[math]}$ 的直径，弦 $\text{[math]}$ 于H，过CD延长线上一点E作 $\text{[math]}$ 的切线交AB的延长线于 $\text{[math]}$ 切点为G，连接AG交CD于K．

(1) 求证： $\text{[math]}$ ；

(2) 若 $\text{[math]}$ ，试判断AC与EF的位置关系，并说明理由；

(3) 在 $\text{[math]}$ 的条件下，若 $\text{[math]}$ ， $\text{[math]}$ ，求FG的长．

综合题困难

3. 如图，AB是⊙O的直径，PB与⊙O相切于点B，连接PA交⊙O于点C，连接BC．

(1) 求证：∠BAC=∠CBP；

(2) 求证：PB²=PC•PA；

(3) 当AC=6，CP=3时，求sin∠PAB的值．

综合题困难