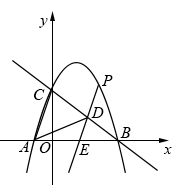
如图，抛物线y=﹣ x2+ x+3 与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，连接AC、BC．点P沿AC以每秒1个单位长度的速度由点A向点C运动，同时，点Q沿BO以每秒2个单位长度的速度由点B向点O运动，当一个点停止运动时，另一个点也随之停止运动，连接PQ．过点Q作QD⊥x轴，与抛物线交于点D，与BC交于点E，连接PD，与BC交于点F．设点P的运动时间为t秒（t＞0）．

0 返回出卷网首页

1. 如图，抛物线y=﹣ $\text{[math]}$ x²+ $\text{[math]}$ x+3 $\text{[math]}$ 与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，连接AC、BC．点P沿AC以每秒1个单位长度的速度由点A向点C运动，同时，点Q沿BO以每秒2个单位长度的速度由点B向点O运动，当一个点停止运动时，另一个点也随之停止运动，连接PQ．过点Q作QD⊥x轴，与抛物线交于点D，与BC交于点E，连接PD，与BC交于点F．设点P的运动时间为t秒（t＞0）．

(1) 求直线BC的函数表达式；

(2) ①直接写出P，D两点的坐标（用含t的代数式表示，结果需化简）

②在点P、Q运动的过程中，当PQ=PD时，求t的值；

(3) 试探究在点P，Q运动的过程中，是否存在某一时刻，使得点F为PD的中点？若存在，请直接写出此时t的值与点F的坐标；若不存在，请说明理由．

【考点】

二次函数图象与坐标轴的交点问题; 锐角三角函数的定义; 求特殊角的三角函数值; 二次函数与一次函数的综合应用; 二次函数-动态几何问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 综合与探究

如图，二次函数 $\text{[math]}$ 与 $\text{[math]}$ 轴交于 $\text{[math]}$ ， $\text{[math]}$ 两点，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ．点 $\text{[math]}$ 是射线 $\text{[math]}$ 上的动点，过点 $\text{[math]}$ 作 $\text{[math]}$ ，并且交 $\text{[math]}$ 轴于点 $\text{[math]}$ ．

(1) 请直接写出 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三点的坐标及直线 $\text{[math]}$ 的函数表达式；

(2) 当 $\text{[math]}$ 平分 $\text{[math]}$ 时，求出点 $\text{[math]}$ 的坐标；

(3) 当点 $\text{[math]}$ 在线段 $\text{[math]}$ 上运动时，直线 $\text{[math]}$ 与抛物线在第一象限内交于点 $\text{[math]}$ ，则线段 $\text{[math]}$ 是否存在最大值？若存在，求出其最大值；若不存在，请说明理由．

综合题困难

2. 在平面直角坐标系中，已知抛物线 $\text{[math]}$ 与x轴交A，B两点（点A在点B的左侧），与y轴交于点C，顶点为点D．

(1) 当 $\text{[math]}$ 时，求点A，B，C，D的坐标：

(2) 如图1，直线DC交x轴于点E，若 $\text{[math]}$ ，求m的值及直线DE的表达式；

(3) 如图2，在（2）的条件下，若点F为OC的中点，连接AF，动点P在第二象限的抛物线上运动，过点P作x轴的垂线，垂足为点H，交AF于点G，过点G作GM⊥DE于点M，求 $\text{[math]}$ 的最大值．

综合题困难

3. 平面直角坐标系中，抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 两点，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ．

(1) 求抛物线的解析式，并直接写出点 $\text{[math]}$ ， $\text{[math]}$ 的坐标；

(2) 在抛物线的对称轴上是否存在点 $\text{[math]}$ ，使 $\text{[math]}$ 是直角三角形？若存在，请直接写出点 $\text{[math]}$ 的坐标，若不存在，请说明理由；

(3) 如图，点 $\text{[math]}$ 是直线 $\text{[math]}$ 上的一个动点，连接 $\text{[math]}$ ， $\text{[math]}$ ，是否存在点 $\text{[math]}$ 使 $\text{[math]}$ 最小，若存在，请求出点 $\text{[math]}$ 的坐标，若不存在，请说明理由；

综合题困难