如图，将▱ABCD沿过点A的直线l折叠，使点D落到AB边上的点D′处，折痕l交CD边于点E，连接BE．

0 返回出卷网首页

1. 如图，将▱ABCD沿过点A的直线l折叠，使点D落到AB边上的点D′处，折痕l交CD边于点E，连接BE．

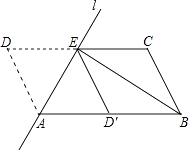
(1) 求证：四边形BCED′是平行四边形；

(2) 若BE平分∠ABC，求证：AB²=AE²+BE² ．

【考点】

勾股定理; 平行四边形的判定与性质; 翻折变换（折叠问题）;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，将 $\text{[math]}$ 沿过点 $\text{[math]}$ 的直线 $\text{[math]}$ 折叠，使点 $\text{[math]}$ 落到 $\text{[math]}$ 边上的 $\text{[math]}$ 处，折痕交 $\text{[math]}$ 边于点 $\text{[math]}$ ，连接 $\text{[math]}$ .

(1) 求证：四边形 $\text{[math]}$ 是平行四边形；

(2) 若 $\text{[math]}$ 平分 $\text{[math]}$ ，求证： $\text{[math]}$ .

综合题普通

2. 在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 分别为边 $\text{[math]}$ 上异于端点的动点，且 $\text{[math]}$ ，连结 $\text{[math]}$ ，将四边形 $\text{[math]}$ 沿着 $\text{[math]}$ 折叠得到四边形 $\text{[math]}$ ．

(1) 如图1，边 $\text{[math]}$ ， $\text{[math]}$ 交于点 $\text{[math]}$ ，若 $\text{[math]}$ ，求证：四边形 $\text{[math]}$ 为平行四边形；

(2) 如图2，当点 $\text{[math]}$ 落在点 $\text{[math]}$ 处时，求折痕 $\text{[math]}$ 的长；

(3) 当点 $\text{[math]}$ 落在 $\text{[math]}$ 的边上时，求点 $\text{[math]}$ 之间的距离．

综合题困难

3. 如图，平行四边形 $\text{[math]}$ 中， $\text{[math]}$ 是它的一条对角线，过 $\text{[math]}$ 、 $\text{[math]}$ 两点作 $\text{[math]}$ ，垂足分别为 $\text{[math]}$ 、 $\text{[math]}$ ，延长 $\text{[math]}$ 、 $\text{[math]}$ 分别交 $\text{[math]}$ 、 $\text{[math]}$ 于 $\text{[math]}$ 、 $\text{[math]}$ ．

(1) 求证：四边形 $\text{[math]}$ 是平行四边形；

(2) 已知 $\text{[math]}$ ．求 $\text{[math]}$ 的长．

综合题普通