0 返回出卷网首页
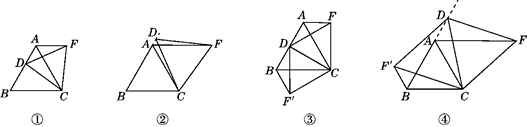
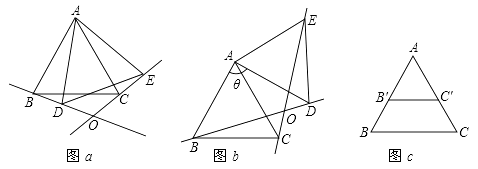
1. 如图1，等边△ABC中，CE平分∠ACB，D为BC边上一点，且DE=CD，连接BE．

(1) 若CE=4，BC= ，求线段BE的长；
(2) 如图2，取BE中点P，连接AP，PD，AD，求证：AP⊥PD且AP= PD；

(3) 如图3，把图2中的△CDE绕点C顺时针旋转任意角度，然后连接BE，点P为BE 中点，连接AP，PD，AD，问第（2）问中的结论还成立吗？若成立，请证明；若不成立，请说明理由．

【考点】
全等三角形的判定与性质; 等边三角形的性质; 旋转的性质;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 在△ABC中，AB=AC，∠BAC=α（0°＜α＜60°），将线段BC绕点B逆时针旋转60°得到线段BD．

(1) 如图1，直接写出∠ABD的大小（用含α的式子表示）；
(2) 如图2，∠BCE=150°，∠ABE=60°，判断△ABE的形状并加以证明；
(3) 在（2）的条件下，连接DE，若∠DEC=45°，求α的值．
综合题 普通
2. 如图，已知∠DAC＝90°，△ABC是等边三角形，点P为射线AD上任意一点（点P与点A不重合），连接CP ， 将线段CP绕点C顺时针旋转60°得到线段CQ ， 连接QB并延长交直线AD于E ．

(1) 如图1，猜想∠QEP＝；
(2) 如图2，若当∠DAC是锐角时，其他条件不变，猜想∠QEP的度数，并证明；
(3) 如图3，若∠DAC＝135°，∠ACP＝15°，且AC＝6，求BQ的长．
综合题 困难
3. 如图
(1) 操作发现：如图①，D是等边三角形ABC边BA上一动点(点D与点B不重合)，连接DC，以DC为边在DC上方作等边三角形DCF，连接AF.你能发现线段AF与BD之间的数量关系吗？并证明你发现的结论.
(2) 类比猜想：如图②，当动点D运动至等边三角形ABC边BA的延长线上时，其他作法与(1)相同，猜想AF与BD在(1)中的结论是否仍然成立？
(3) 深入探究：

Ⅰ.如图③，当动点D在等边三角形ABC边BA上运动时(点D与点B不重合)，连接DC，以DC为边在DC上方、下方分别作等边三角形DCF和等边三角形DCF′，连接AF、BF′，探究AF、BF′与AB有何数量关系？并证明你探究的结论.

Ⅱ.如图④，当动点D在等边三角形边BA的延长线上运动时，其他作法与图③相同，Ⅰ中的结论是否成立？若不成立，是否有新的结论？并证明你得出的结论.
综合题 困难