1.
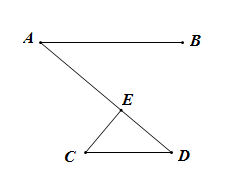
在数学学习中整体思想与转化思想是我们常用到的数学思想.如图(1)中,求∠A+∠B+∠C+∠D+∠E的度数等于多少时,我们可以连接CD,利用三角形的内角和则有∠B+∠E=∠ECD+∠BDC,这样∠A、∠B、∠C、∠D、∠E的和就转化到同一个△ACD中,即∠A+∠B+∠C+∠D+∠E=180°.

尝试练习:
图(2)中∠A+∠B+∠C+∠D+∠E的度数等于.
图(3)中∠A+∠B+∠C+∠D+∠E的度数等于.
图(4)中∠A+∠B+∠C+∠D+∠E+∠F的度数等于.
【考点】
三角形内角和定理;
基础巩固
能力提升
变式训练
拓展培优
真题演练