1.
定义:先将△ABC以点A为位似中心放大或缩小,接着将所得三角形以点A为旋转中心,逆时针旋转一个角度α后,得到△ADE,则我们称△ABC与△ADE互为“旋转相似三角形”.
理解:
(1)
如图1,△ABC与△ADE互为“旋转相似三角形”.若α=20°,∠D=100°,∠C=30°,则∠BAE的度数为;
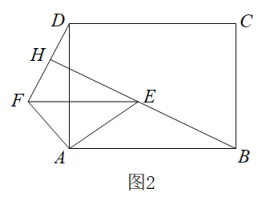
(2)
如图2,在等腰△ABC中,AB=AC,∠BAC=120°,AD是高,点E为DC上一动点,以线段AE为斜边在右侧作Rt△AEF , 使∠AFE=90°,∠AEF=30°,连接DF,求证:△ABE与△ADF互为“旋转相似三角形”;
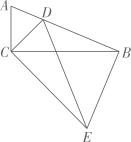
(3)
如图3,△ABC与△ADE互为“旋转相似三角形”,连接BD、CE,若∠ABC+∠ADC
=90°,AB=2AC,DE=3,CD=4,求BD的长
运用:
【考点】
相似三角形的判定与性质;
旋转的性质;
能力提升
真题演练