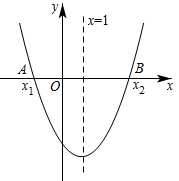
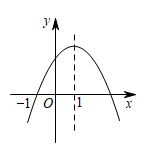1.
已知二次函数 
（其中 
是常数）
(1)
已知函数过点 
，求出b和c满足的关系式；
(2)
若 
，求证：不论b为何值，该函数图象与x轴一定有交点；
(3)
四位同学在研究此函数时，甲发现当 
时， 
；乙发现函数的最大值是9；丙发现函数图象的对称轴是 
；丁发现 
是方程 
的一个根.已知这四位同学中只有一位发现的结论是错误的，请直接写岀错误的那个同学是谁，并根据另三位同学的表述求出此函数表达式.
【考点】
二次函数的最值;
二次函数图象与坐标轴的交点问题;
