0 返回出卷网首页
1. 如图，在4×3正方形网格中，每个小正方形的边长都是1.

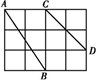
(1) 分别求出线段AB，CD的长度；
(2) 在图中画线段EF，使得EF的长为 ，以AB，CD，EF三条线段能否构成直角三角形，并说明理由.
【考点】
勾股定理; 勾股定理的逆定理;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 如图，连接四边形ABCD的对角线AC，已知∠B=90°，BC=3，AB=4，CD=5，AD= ．

求证：

 

(1) AC=CD；
(2) △ACD是直角三角形．
综合题 普通
2. 我市某中学有一块四边形的空地ABCD，如图所示，为了绿化环境，学校计划在空地上种植草皮，经测量∠A=90°，AB=3m，DA=4m，BC=12m，CD=13m.

(1) 求出空地ABCD的面积.
(2) 若每种植1平方米草皮需要200元，问总共需投入多少元？
综合题 普通
3. 如图，在4x4的正方形网格中，每个小正方形的边长都为1.

求：

(1) △ABC的周长；
(2) ∠ABC度数.
综合题 普通