如图，点E、F为线段BD的两个三等分点，四边形AECF是菱形．

0 返回出卷网首页

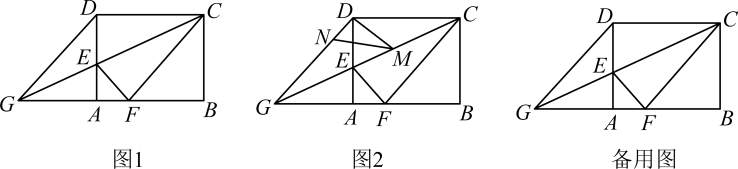
1. 如图，点E、F为线段BD的两个三等分点，四边形AECF是菱形．

(1) 试判断四边形ABCD的形状，并加以证明；

(2) 若菱形AECF的周长为20，BD为24，试求四边形ABCD的面积．

【考点】

勾股定理; 菱形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 为边 $\text{[math]}$ 上的中线，点E与点D关于直线 $\text{[math]}$ 对称，连接 $\text{[math]}$ ， $\text{[math]}$ ．

(1) 求证：四边形 $\text{[math]}$ 是菱形；

(2) 连接BE，若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．

综合题普通

2. 如图，在四边形ABCD中，AB∥DC，AB＝AD，对角线AC．BD交于点O，AC平分∠BAD，过点C作CE⊥AB交AB的延长线于点E．连接OE．

(1) 求证：四边形ABCD是菱形；

(2) 若AE＝5，OE＝3，求线段CE的长．

综合题普通

3. 已知：线段a，b.

(1) 尺规作图：作出一个菱形，使它的边长为a，另一条对角线为b（要求：保留作图痕迹，不写作法）；

(2) 若a＝5，b＝8，求该菱形的高线长.

综合题普通