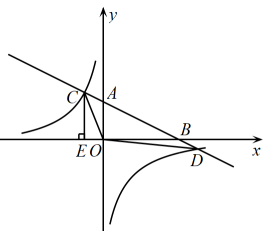
如图，一次函数y＝kx+b（k＜0）的图象与反比例函数y＝图象都经过点A（a，4），一次函数y＝kx+b（k＜0）的图象经过点C（3，0），且与两坐标轴围成的三角形的面积为3．

0 返回出卷网首页

1. 如图，一次函数y＝kx+b（k＜0）的图象与反比例函数y＝ $\text{[math]}$ 图象都经过点A（a，4），一次函数y＝kx+b（k＜0）的图象经过点C（3，0），且与两坐标轴围成的三角形的面积为3．

(1) 求这两个函数的表达式；

(2) 将直线AB向下平移5个单位长度后与第四象限内的反比例函数图象交于点D，连接AD、BD，求△ADB的面积．

【考点】

反比例函数与一次函数的交点问题; 三角形的面积; 平移的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，一次函数 $\text{[math]}$ 与函数为 $\text{[math]}$ 的图象交于 $\text{[math]}$ 两点．

(1) 求这两个函数的解析式；

(2) 根据图象，直接写出满足 $\text{[math]}$ 时x的取值范围；

(3) 点P在线段 $\text{[math]}$ 上，过点P作x轴的垂线，垂足为M，交函数 $\text{[math]}$ 的图象于点Q，若 $\text{[math]}$ 面积为3，求点P的坐标．

综合题普通

2. 如图，已知一次函数y=x﹣2与反比例函数y= $\text{[math]}$ 的图象交于A、B两点．

(1) 求A、B两点的坐标；

(2) 观察图象，直接写出一次函数值小于反比例函数值的x的取值范围；

(3) 坐标原点为O，求△AOB的面积．

综合题普通

3. 如图，一次函数 $\text{[math]}$ 的图象与反比例函数 $\text{[math]}$ 的图象交于 $\text{[math]}$ 两点，与 $\text{[math]}$ 轴交于 $\text{[math]}$ 两点， $\text{[math]}$ 轴于点 $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ ．

(1) 求一次函数的解析式和反比例函数的解析式

(2) 求 $\text{[math]}$ 的面积；

(3) 根据图象直接写出一次函数的值大于反比例函数的值时，自变量 $\text{[math]}$ 的取值范围．

综合题困难