0 返回出卷网首页
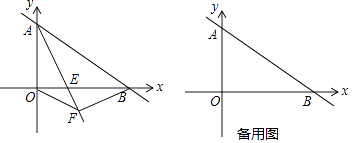
1. 如图①，OP为一墙面，它与地面OQ垂直，有一根木棒AB如图放置，点C是它的中点，现在将木棒的A点在OP上由A点向下滑动，点B由O点向OQ方向滑动，直到AB横放在地面为止．

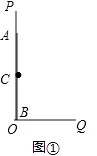
(1) 在AB滑动过程中，点C经过的路径可以用下列哪个图象来描述（   ）
(2) 若木棒长度为2m，如图②射线OM与地面夹角∠MOQ=60°，当AB滑动过程中，与OM并于点D，分别求出当AD= 、AD=1、AD= 时，OD的值．
(3) 如图③，是一个城市下水道，下水道入口宽40cm，下水道水平段高度为40cm，现在要想把整根木棒AB通入下水道水平段进行工作，那么这根木棒最长可以是（cm）（直接写出结果，结果四舍五入取整数）．
【考点】
相似三角形的性质;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，点P从点A出发沿边AC向点C以每秒1个单位长度的速度运动，同时点Q从点C出发沿边CB向点B以每秒a个单位长度的速度运动，过点P作PD⊥BC，交AB于点D，连接PQ．当其中一点到达端点时，另一点也随之停止运动，设运动时间为t秒（t≥0）．

(1) 当a=2时，解答下列问题：

①QB=，PD=．（用含t的代数式分别表示）
(2) 当a为某个数值时，四边形PDBQ在某一时刻为菱形，求a的值及四边形PDBQ为菱形时t的值．
(3) 当t=2时，在整个运动过程中，恰好存在线段PQ的中点M到△ABC三边距离相等，直接写出此刻a的值．
综合题 普通
2. 如图，已知直线l1∥l2 ， 线段AB在直线l1上，BC垂直于l1交l2于点C，且AB=BC，P是线段BC上异于两端点的一点，过点P的直线分别交l2、l1于点D、E（点A、E位于点B的两侧），满足BP=BE，连接AP、CE．

(1) 求证：△ABP≌△CBE；
(2) 连结AD、BD，BD与AP相交于点F．如图2．

①当 =2时，求证：AP⊥BD；

②当 =n（n＞1）时，设△PAD的面积为S1 ， △PCE的面积为S2 ， 求 的值．
综合题 普通
3. 已知一次函数y=﹣ x+6的图象与坐标轴交于A、B点（如图），AE平分∠BAO，交x轴于点E．

(1) 求点B的坐标；
(2) 求直线AE的表达式；
(3) 过点B作BF⊥AE，垂足为F，连接OF，试判断△OFB的形状，并求△OFB的面积．
综合题 普通