1.
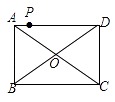
如图,矩形ABCD的对角线AC、BD交于点O,点P在边AD上从点A到点D运动,过点P作PE⊥AC于点E,作PF⊥BD于点F,已知AB=3,AD=4,随着点P的运动,关于PE+PF的值,下面说法正确的是( )

A.
先增大,后减小
B.
先减小,后增大
C.
始终等于2.4
D.
始终等于3
【考点】
三角形的面积;
矩形的性质;