组卷在线网-ZUJUAN.COM

0 返回出卷网首页

1.

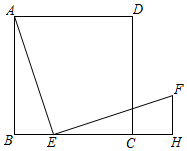
(1) 如图1，在正方形ABCD中，EF分别是BC，CD上的点，且∠EAF＝45°，探究图中线段BE，EF，FD之间的数量关系.小王同学探究此问题的方法是将△ABE绕A点旋转90°使得B与D重合，连接AG，由此得到，再证明，可得出结论，他的结论应是.

(2) 拓展延伸：

如图2，等腰直角三角形ABC中，∠ABC＝90°，AB＝BC，点G，H在边AC上，且∠GBH＝45°，写出图中线段AG，GH，CH之间的数量关系并证明.

【考点】

勾股定理; 正方形的性质; 旋转的性质; 三角形全等的判定-SAS;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

(1) 如图1，在正方形ABCD中，点E、F分别是BC、CD边上的动点，且 $\text{[math]}$ ，求证： $\text{[math]}$ .

(2) 如图2，在正方形 $\text{[math]}$ 中，如果点 $\text{[math]}$ 、 $\text{[math]}$ 分别是 $\text{[math]}$ 、 $\text{[math]}$ 延长线上的动点，且 $\text{[math]}$ ，则 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 之间数量关系是什么？请写出证明过程.

(3) 如图1，若正方形 $\text{[math]}$ 的边长为6， $\text{[math]}$ ，求 $\text{[math]}$ 的长.

综合题困难

2. 如图，正方形 $\text{[math]}$ 中， $\text{[math]}$ 4 ，动点 $\text{[math]}$ 从点 $\text{[math]}$ 出发沿 $\text{[math]}$ 向点 $\text{[math]}$ 运动，连结 $\text{[math]}$ ，以 $\text{[math]}$ 为边在其右侧作正方形 $\text{[math]}$ 与 $\text{[math]}$ 相交于点 $\text{[math]}$ ．

(1) 在点 $\text{[math]}$ 的运动过程中，点 $\text{[math]}$ 的位置也随之改变，则点 $\text{[math]}$ 始终在直线 $\text{[math]}$ 上吗？如果在，请给出证明，如果不在，请说明理由．

(2) 当点 $\text{[math]}$ 在 $\text{[math]}$ 边上运动时， $\text{[math]}$ 的面积如何变化？请写出推理过程．

综合题普通

3. 如图，点E是正方形ABCD的边BC上的动点， $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ .

(1) 求证： $\text{[math]}$ ；

(2) 若 $\text{[math]}$ ， $\text{[math]}$ ，用x表示DF的长.

综合题普通